引言：

K-Means是一种经典的聚类算法，被广泛应用于数据挖掘、图像处理和机器学习等领域。它的原理简单但功能强大，能够将数据集划分成不同的簇，每个簇内的数据点相似度较高，而不同簇之间的数据点相似度较低。本文将介绍K-Means算法的基本概念和原理。

K-Means算法原理：

K-Means算法的基本原理是：通过迭代的方式，将数据点划分到最接近的类簇中心点所代表的类簇中，然后根据每个类簇内的所有点重新计算该类簇的中心点（取平均值），再不断重复此过程，直至类簇中心点的变化很小或达到指定的迭代次数。

• 聚类数目（K）的选择： K-Means算法的第一步是确定要将数据划分成多少个簇。这个选择通常基于领域知识或使用Elbow方法等统计技巧来确定。K的选择对于聚类结果有着重要的影响。如果K选择过小，可能会导致簇的划分不够细致，无法准确地反映数据的结构；如果K选择过大，可能会导致簇的划分过于细致，会被数据的噪声影响，导致分类不准确。
• 距离的度量： K-Means使用欧式距离（Euclidean distance）来度量数据点之间的相似性，但也可以根据具体问题选择其他距离度量方法。
• 质心： 每个簇都有一个质心，它是该簇内所有数据点的均值。质心代表了簇的中心位置。
• 优化目标： K-Means的优化目标是最小化每个数据点到其所属簇质心的距离之和。

K-Means算法步骤：

这里我们将数据可视化，以便更好的解释k-Means聚类的过程，想要自己体验的小伙伴可以点击这里查看：

K-means聚类可视化网址

让我们先看看需要进行分类的数据（未处理）：

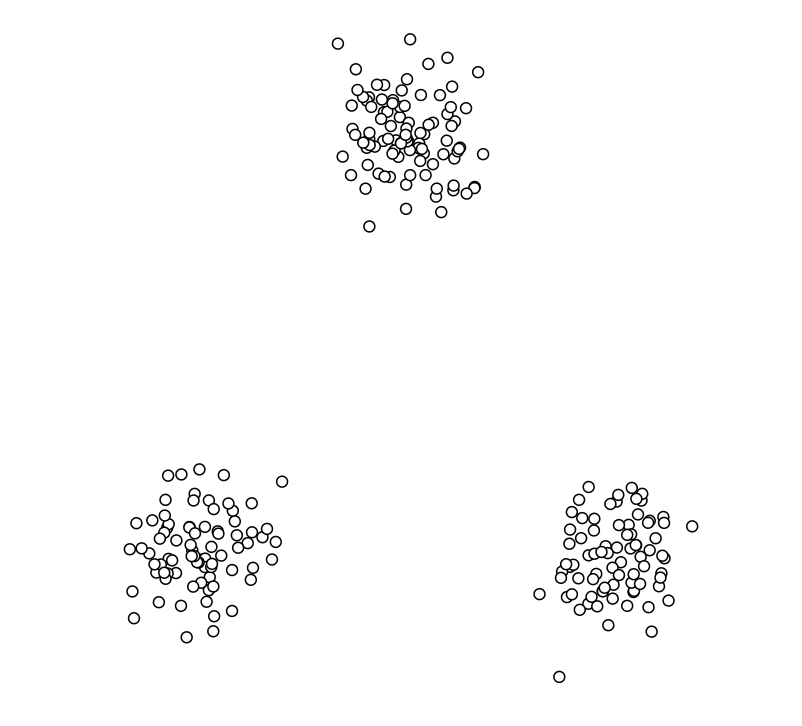
1.首先，选择k个初始聚类中心点（可以随机选择或根据经验选择，这里的k设置为3）。这里我们初始了三个聚类中心点（红绿蓝）

2.针对每个数据点，计算其与k个聚类中心点的距离（这里的k设置为3），将其归为距离最近的聚类中心点所在的类。这里可以看到数据被分为红绿蓝三个类别，加粗的为初始聚类中心点

3.计算每个聚类中心点所在类的数据点的平均值，将其作为新的聚类中心点。经过再一次计算，发现聚类中心点已经改变位置，所以接下来我们要重新根据欧式距离（Euclidean distance）来度量数据点之间的相似性，重新分成三个簇。

4.重复步骤2和步骤3，直到聚类中心点不再发生变化或已达到预先设定的停止条件。这里一共迭代了四次就成功将数据分为三类簇。

5.最终将数据集划分为k个不同的类。

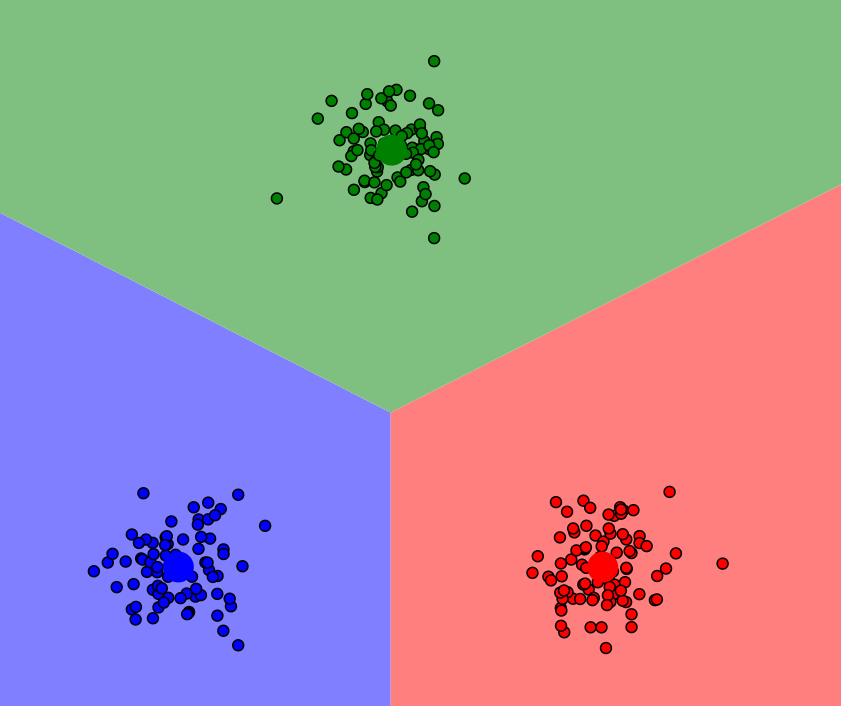
结论：

K-Means算法是一个强大的聚类工具，因为他属于无监督学习，所以能够帮助我们发现数据集中的隐藏模式和结构。但是，正确选择聚类数目和合适的初始质心对算法的性能至关重要。此外，K-Means也可以通过优化方法进行改进，以获得更好的聚类结果。

原文链接：https://blog.csdn.net/AI_dataloads/article/details/133322550      K-Means聚类算法原理（可视化超详细）

https://blog.csdn.net/qq_38614074/article/details/137456095   【机器学习-14】K-means聚类算法：原理、应用与优化