作为一个网安专业的学子,传统方面的安全还是得有所涉及,就写两篇SHA256和椭圆曲线密码学ECC:
椭圆曲线的链接:ECC椭圆曲线密码学的原理、公式推导、例子 – Forever
SHA256算法可视化(科学上网):Sha256 Algorithm Explained
SHA256在线加密工具:SHA256 在线加密工具 | 菜鸟工具
SHA256在区块链和比特币中非常重要,具体可见:np问题、区块链、比特币 – Forever
学习区块链,总是无法避开各种加密算法,因为各种加密算法在实现区块链当中的各个环节都有着不可替代的作用。这里介绍一下在比特币挖矿以及merkle树当中被大量使用的鼎鼎大名的SHA256算法。
1、SHA-2 族算法简介
一个n位的哈希函数就是一个从任意长的消息到n位哈希值的映射,一个n位的加密哈希函数就是一个单向的、避免碰撞的n位哈希函数。这样的函数是目前在数字签名和密码保护当中极为重要的手段。
当前比较流行的哈希函数主要有128位的MD4和MD5和160位的SHA-1,今天介绍的SHA-2族有着更多位的输出哈希值,破解难度更大,能够提高更高的安全性。
SHA-2,名称来自于安全散列算法2(英语:Secure Hash Algorithm 2)的缩写,一种密码散列函数算法标准,由美国国家安全局研发,由美国国家标准与技术研究院(NIST)在2001年发布。属于SHA算法之一,是SHA-1的后继者。其下又可再分为六个不同的算法标准,包括了:SHA-224、SHA-256、SHA-384、SHA-512、SHA-512/224、SHA-512/256。
这些变体除了生成摘要的长度、循环运行的次数等一些细微差异之外,基本结构是一致的。本文主要讲一讲SHA256。
2、SHA256原理详解
(1)概述
对于任意长度的消息,SHA256都会产生一个256位的哈希值,称作消息摘要。这个摘要相当于是个长度为32个字节的数组,通常有一个长度为64的十六进制字符串来表示,其中1个字节=8位,一个十六进制的字符的长度为4位。
来看一个具体的例子:
BlockChain
这句话经过哈希函数SHA256后得到的哈希值为:
3a6fed5fc11392b3ee9f81caf017b48640d7458766a8eb0382899a605b41f2b9
总体上,HSA256与MD4、MD5以及HSA-1等哈希函数的操作流程类似,待哈希的消息在继续哈希计算之前首先要进行以下两个步骤:
- 对消息进行补位处理,是的最终的长度是512位的倍数,然后
- 以512位为单位对消息进行分块为$M^{(1)},M^{(2)},\ldots,M^{(N)}$
消息区块将进行逐个处理:从一个固定的初始哈希$H^{(0)}$开始,进行以下序列的计算:
$H^{(i)}=H^{(i-1)}+C_{M^{(i)}}(H^{(i-1)})$
其中$C$是SHA256的压缩函数,$+$是mod $2^{32}$加法,即将两个数字加在一起,如果对$2^{32}$取余,$H^{(N)}$是消息区块的哈希值。
(2)算法详细描述
SHA256的压缩函数主要对512位的消息区块和256位的中间哈希值进行操作,本质上,它是一个通过将消息区块为密钥对中间哈希值进行加密的256位加密算法。 因此,为了描述SHA256算法,有以下两方面的组件需要描述:
- SHA256压缩函数
- SHA256消息处理流程
以下的描述当中所使用到的标记如下:
- $\oplus$:按位异或
- $\wedge$:按位与
- $\lor$:按位或
- $\neg$:补位
- +:相加以后对$2^{32}$求余
- $R^n$:右移n位
- $S^n$:循环右移n位
以上所有的操作都是针对32位字节。
a.常量初始化
初始哈希值$H^{(0)}$取自自然数中前面8个素数(2,3,5,7,11,13,17,19)的平方根的小数部分, 并且取前面的32位。下面举个例子: $\sqrt{2}$小数部分约为0.414213562373095048, 而其中
$0.414213562373095048\approx6*16^{-1}+a*16^{-2}+0*16^{-3}+\ldots$
于是,质数2的平方根的小数部分取前32位就对应0x6a09e667.
如此类推,初始哈希值$H^{(0)}$由以下8个32位的哈希初值构成:
$\begin{gathered}
H_{1}^{(0)}=6a09e667 \\
H_{2}^{(0)}=bb67ae85 \\
H_{3}^{(0)}=3c6ef372 \\
H_{4}^{(0)}=a54ff53a \\
H_{5}^{(0)}=510e527f \\
H_{6}^{(0)}=9b05688c \\
H_{7}^{(0)}=1f83d9ab \\
H_{8}^{(0)}=5be0cd19
\end{gathered}$
SHA256算法当中还使用到64个常数, 取自自然数中前面64个素数的立方根的小数部分的前32位, 如果用16进制表示, 则相应的常数序列如下:
428a2f98 71374491 b5c0fbcf e9b5dba5 3956c25b 59f111f1 923f82a4 ab1c5ed5 d807aa98 12835b01 243185be 550c7dc3 72be5d74 80deb1fe 9bdc06a7 c19bf174 e49b69c1 efbe4786 0fc19dc6 240ca1cc 2de92c6f 4a7484aa 5cb0a9dc 76f988da 983e5152 a831c66d b00327c8 bf597fc7 c6e00bf3 d5a79147 06ca6351 14292967 27b70a85 2e1b2138 4d2c6dfc 53380d13 650a7354 766a0abb 81c2c92e 92722c85 a2bfe8a1 a81a664b c24b8b70 c76c51a3 d192e819 d6990624 f40e3585 106aa070 19a4c116 1e376c08 2748774c 34b0bcb5 391c0cb3 4ed8aa4a 5b9cca4f 682e6ff3 748f82ee 78a5636f 84c87814 8cc70208 90befffa a4506ceb bef9a3f7 c67178f2
b.消息预处理
在计算消息的哈希摘要之前需要对消息进行预处理:
对消息进行补码处理: 假设消息$M$的二进制编码长度为 $l$位. 首先在消息末尾补上一位”1″, 然后再补上k个”0″, 其中$k$为下列方程的最小非负整数
$l+1+k\equiv448\quad\mathrm{mod~}512$
举个例子, 以消息”abc”为例显示补位的过程.
a,b,c对应的ASCII码和二进制编码分别如下:
原始字符 ASCII码 二进制编码
a 97 01100001
b 98 01100010
c 99 01100011因此, 原始信息”abc”的二进制编码为:01100001 01100010 01100011, 第一步补位, 首先在消息末尾补上一位”1″, 结果为: 01100001 01100010 01100011 1; 然后进行第二步的补位, 因为$l=24$, 可以得到$k=423$, 在第一步补位后的消息后面再补423个”0″, 结果如下:
$0110000101100010011000111\underbrace{00…0}_{423}$
最后还需要在上述字节串后面继续进行补码, 这个时候补的是原消息”abc”的二进制长度l=24的64位二进制表示形式, 补完以后的结果如下:
$0110000101100010011000111\underbrace{00…0}_{423}\underbrace{00…011000}_{64}$
最终补完以后的消息二进制位数长度是512的倍数。
这里需要注意的两点是不管原来的消息长度是多少, 即使长度已经满足对512取模后余数是448,补位也必须要进行,这时要填充512位. 另外, 考虑到最后要将消息长度$l$转换为64位二进制编码, 因此, 长度的必须小于$2^{64}$,绝大多数情况, 这个足够大了。
$2^{64}byte = 2^{54}KB = 2^{44}MB= 2^{34}GB= 2^{24}TB$
将补码处理后的消息以512位为单位分块为:$M^{(1)},M^{(2)},\ldots,M^{(N)}$,其中第$i$个消息块的前32位表示为:$M_0^{(i)}$,后面32位为:$M_1^{(i)}$,以此类推,最后32位的消息块可表示为:$M_{15}^{(i)}$.我们采用Big endian约定对数据进行编码,即认为第一个字节是最高位字节,因此,对于每一个32位字节最左边的比特是最大的比特位。
Big endian:大端和小端(Big endian and Little endian) – Forever
c.摘要计算主循环
哈希计算算法如下:
$For$ $i= 1\rightarrow N$ $( N=$补码后消息块个数)
- 用第$(i-1)$个中间哈希值来对 $a,b,c,d,e,f,g,h$进行初始化,当$i=1$时,就使用初始化哈希,即:
\begin{aligned}
& a\leftarrow H_{1}^{(i-1)} \\
& b\leftarrow H_{2}^{(i-1)} \\
& h\leftarrow H_{8}^{(i-1)}
\end{aligned}
- 应用SHA256压缩函数来更新$a,b,\dots , h$
- $For$ $j=0\to63$
-
-
- 计算$Ch(e,f,g),M_{aj}(a,b,c),\Sigma_0(a),\Sigma_1(e),W_j\text{(具体定义如下)}$
-
\begin{aligned}
& \mathrm{T}_1\leftarrow h+\Sigma_1(e)+Ch(e,f,g)+K_j+W_j \\
& \mathrm{T}_2\leftarrow \Sigma_{0}(a) + M_{aj}(a,b,c)\\
& h\leftarrow g \\
& g\leftarrow f \\
& f\leftarrow e \\
& e\leftarrow d+T_1 \\
& d\leftarrow c \\
& c\leftarrow b \\
& b\leftarrow a \\
& a\leftarrow T_1+T_2
\end{aligned}
-
- 计算第$i$个中间哈希值$H^{(i)}$
\begin{aligned}
& H_{1}^{(i)}\leftarrow a+H_{1}^{(i-1)} \\
& H_{2}^{(i)}\leftarrow b+H_{2}^{(i-1)} \\
& H_{8}^{(i)}\leftarrow h+H_{8}^{(i-1)}
\end{aligned}
-
- $H^{(N)}=(H_1^{(N)},H_2^{(N)},\ldots,H_8^{(N)}) $为最终需要的哈希$M$。
d.逻辑函数定义
SHA256算法当中所使用到的6个逻辑函数如下:每个函数都对32位字节进行操纵,并输出32位字节。
$\begin{aligned}
Ch(x,y,z) & =(x\land y)\oplus(\lnot x\land z) \\
M_{aj}(x,y,z) & =(x\wedge y)\oplus(x\wedge z)\oplus(y\wedge z) \\
\Sigma_{0}(x) & =S^2(x)\oplus S^{13}(x)\oplus S^{22}(x) \\
\Sigma_{1}(x) & =S^6(x)\oplus S^{11}(x)\oplus S^{25}(x) \\
\sigma_{0}(x) & =S^7(x)\oplus S^{18}(x)\oplus R^3(x) \\
\sigma_{1}(x) & =S^{17}(x)\oplus S^{19}(x)\oplus R^{10}(x)
\end{aligned}$
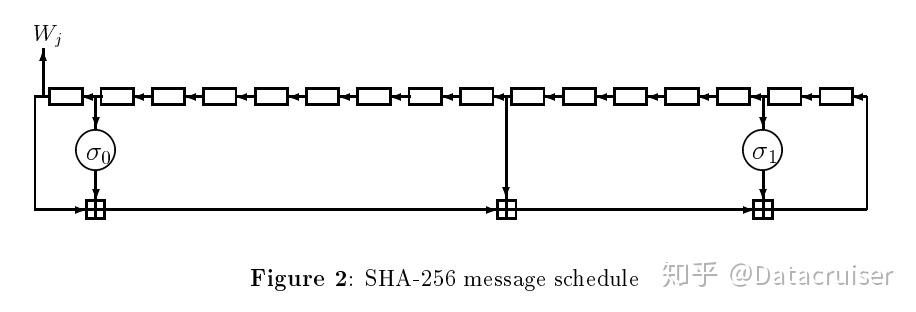
扩展消息块$W_0,W_1,\ldots,W_{63}$通过以下方式进行计算:
$\begin{aligned}
& W_j=M_j^{(i)}for\,j=0,1,\ldots,15 \\
& \quad For \,j=16\to63 \\
& \quad \quad W_j\leftarrow\sigma_1(W_{j-2})+W_{j-7}+\sigma_0(W_{j-15})+W_{j-16}
\end{aligned}$
e.图形表示
SHA256压缩函数的图形表示如下:
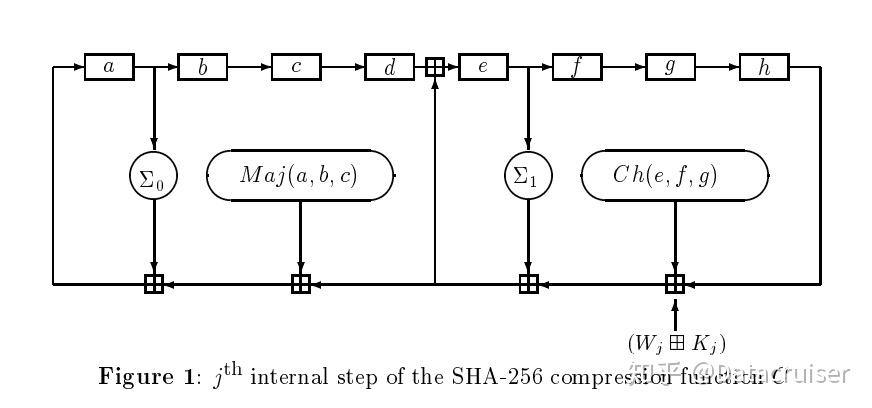
扩展消息块 $W $ 的求解算法可以表示如下: