椭圆曲线具体的原理比较复杂就不讲了。  大概懂了就行

椭圆曲线不是椭圆，就是一条方程或者周长方程类似于椭圆的曲线。

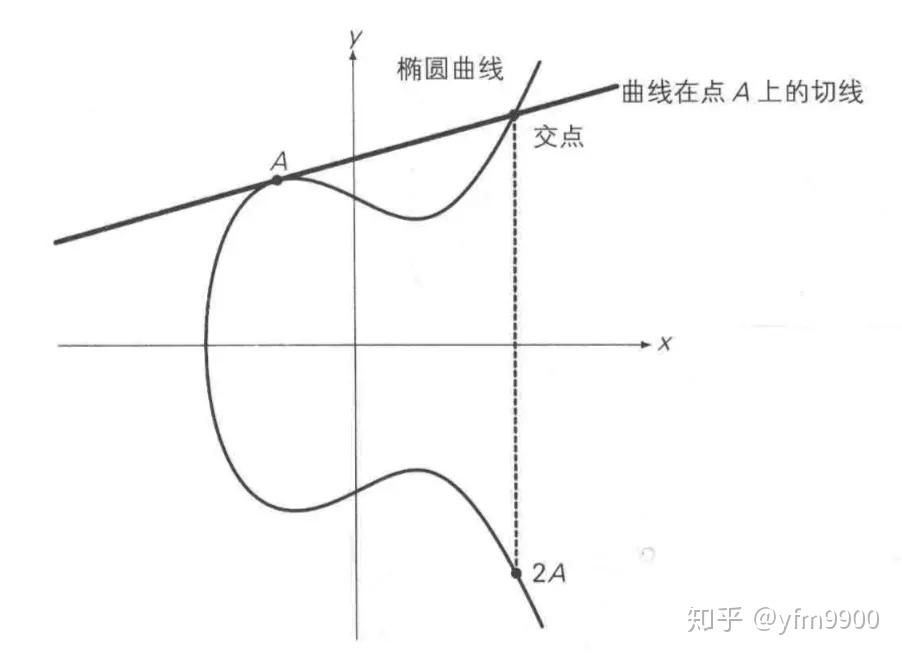
一、椭圆曲线加解密算法原理

设私钥、公钥分别为$d$、$Q$，即$Q = dG$，其中G为基点，椭圆曲线上的已知$G$和$dG$，求$d$是非常困难的，也就是说已知公钥和基点，想要算出私钥是非常困难的。
公钥加密：选择随机数$r$，将消息$M$生成密文$C$，该密文是一个点对，$C = {rG, M+rQ}$，其中$Q$为公钥。
私钥解密：$M + rQ – d(rG) = M + r(dG) – d(rG) = M$，其中$d$、$Q$分别为私钥、公钥。

二、椭圆曲线签名算法原理

椭圆曲线签名算法(ECDSA)。设私钥、公钥分别为$d$、$Q$，即$Q = dG$，其中G为基点。

私钥签名：

• 选择随机数$r$，计算点$rG(x, y)$。
• 根据随机数$r$、消息$M$的哈希$h$、私钥$d$，计算$s = \frac{h+dx}{r}$。
• 将消息$M$、和签名$\{rG, s\}$发给接收方。

公钥验证签名：

• 接收方收到消息$M$、以及签名{$rG=(x,y), s$}。
• 根据消息求哈希$h$。
• 使用发送方公钥$Q$计算：$\frac{hG + xQ}{s}$，并与$rG$比较，如相等即验签成功。
  原理：$\frac{hG + xQ}{s} = \frac{hG + x(dG)}{s} = \frac{(h+xd)G}{s}  = \frac{r(h+xd)G}{h+dx} = rG $

参考链接：椭圆曲线加密算法（ECC） – 知乎