1. 概述
1.1 公钥密码体制的提出
随着计算机与网络技术的飞速发展,保密通信的需求越来越广泛,对称密码体制逐渐表现出以下局限性:
- 密钥分发问题:通信双方要进行加密通信,需要通过秘密的安全信道协商加密密钥,而这种安全信道可能很难实现。
- 密钥管理问题:在$n$个用户的网络中,每个用户要想和其它$n-1$个用户进行通信,须使用$n-1$个密钥,系统的总密钥量将达到$ \frac{n(n-1)}{2} $。密钥的产生、保存、传递、使用和销毁等各个环节中都会变得很复杂,存在着安全隐患。
- 无法实现身份认证和消息的不可否认性
1976年,Whitefield Diffie和MartinHellman《密码学的新方向》(New Directions in Cryptography)中开创性的提出了公钥密码体制,又称非对称密码体制。
该体制中,用户A有一对密钥:加密密钥(公钥)$P_k$和解密密钥(私钥)$ S_k$,两者是不同的,且从加密密钥(公钥)无法推出解密密钥(私钥)。若B要给A发送加密信息,需要在公开目录中查找A的加密密钥(公钥)$P_k$,用它加密消息;A收到密文后,用自己的解密密钥(私钥)$ S_k$解密密文。
在公钥密码体制之前,所有的密码算法都是基于代换和换位两个基本方法,建立在位(字符)方式的操作上。
公钥密码体制为密码学提供了新的理论和技术基础,开创了密码学的新纪元。
- 一方面公钥密码算法是建立在数学函数基础上的,而不是建立在位(字符)方式的操作上的
- 另一方面公钥密码算法是以非对称的形式使用两个密钥,对密钥分配、认证等方面有着深刻的意义。
1.2 公钥密码体制的原理
公钥密码体制的设计最终归结为一个陷门单向函数。陷门单向函数是满足以下条件的函数$f$:
公钥密码体制设计主要考虑以下几个问题:
- 公钥密码体制的安全性依赖的数学难题是什么
- 私有密钥和公开密钥是如何生成的,它们之间有着怎样的关系
- 安全的密钥长度是多少
- 如何实现公钥加密及私钥解密,反之亦然(数字签名)
- 公钥密码体制的安全分析
1.3 常见公钥密码体制
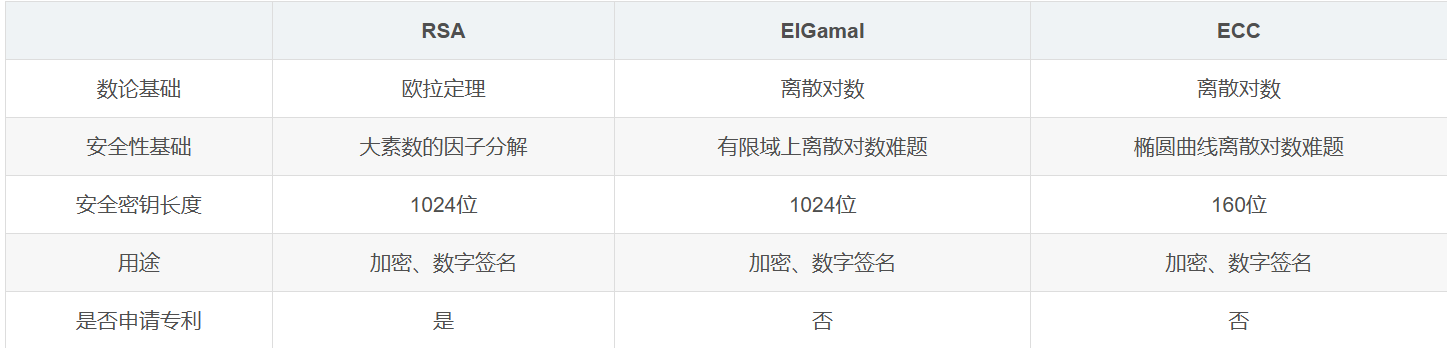
目前应用最广的公钥密码体制主要有3个:
- 基于大整数因子分解问题的RSA公钥密码体制
- 基于有限域乘法群上的离散对数问题的ElGamal公钥密码体制
- 基于椭圆曲线上离散对数问题的椭圆曲线公钥密码体制
此外,还有基于概率的平方剩余问题的公钥密码、基于格的短向量问题的公钥密码、基于余代数编码中的线性解码问题的公钥密码体制等。
2. RSA公钥密码
1978年,美国麻省理工学院的Rivest、Shamir、Adleman联合提出了RSA公钥密码体制,是第一个安全、实用的公钥码算法,已经成为公钥密码的国际标准,得到了广泛应用。
RSA的基础是数论的欧拉定理,其安全性依赖于大整数因子分解的困难性。RSA公钥密码体制可用于加密,也可用于数字签名,且具有安全、易实现等特点。
2.1 RSA密码体制
(1)公私密钥对生成
选取两个大素数$p$、$q$(不可泄露),计算$n=pq$及$n$的欧拉函数$\varphi(n)=(p-1)(q-1)$。
随机选取整数$e(1<e<\varphi(n))$作为公钥,满足$gcd(e,\varphi(n))=1$,即$e$与$\varphi(n)$互素。
使用$Euclid$扩展算法计算私钥$d\equiv e^{-1}$ mod $\varphi(n)$,即$e$的逆元。
(2)加解密算法
- 公钥:$(e,n)$
- 私钥:$d$
- 加密:$c\equiv m^e$ mod $n$
- 解密:$m\equiv c^d$ mod $n$
(3)参数选择
素数 $p$ 和 $q$ 的选取应满足以下要求
- 为避免椭圆曲线因子分解法,$p$ 和 $q$ 的长度相差不能太大。如使用1024bit的数 $n$ ,则 $p$ 和 $q$ 的模长都大致在512bit
- $p$ 和 $q$ 差值不应该太小。如果 $p-q$ 太小,则 $p\approx q$ ,因此 $p\approx\sqrt n$ ,故 $n$ 可以简单地用所有接近 $\sqrt n$ 的奇整数试除而被有效分解
- $gcd(p-1,q-1)$ 应该尽可能小,从而减少不动点个数。
- $ p$ 和$ q$ 应为强素教,即 $p-1$ 和 $q-1$ 都应有大的素因子。
另外,为了防止低指数攻击,$ e$ 和$ d$ 不能选取太小的数。
2.2 RSA公钥密码安全性
RSA密码体制的安全性主要依赖于整数因子分解问题,分解模数$n$的素因子是攻击RSA最直接的方法。如果能够对模数$n$进行分解,便可算出$\varphi(n)=(p-1)(q-1)$,公钥$d$关于私钥$e$满足:$d\times e=1mod(\varphi(n))$,便不难求出私钥$e$,从而破解RSA公钥密码体制。
较早的因子分解分析法是试除法,基本思想是一个密码分析者完全尝试小于$n$的所有素数,直到因子找到。根据素数理论,尝试的次数上限为$\frac{2\sqrt{n}}{\log\sqrt{n}}$。但是对于大数$n$,这种方法的资源消耗在现实中是不可能实现的。
后来出现了一些比较重要的因子分解分析法,包括Pollard在1974年提出的$p-1$因子分解法、Williams提出的$p+1$因子分解法、二次筛(Quadratic Sieve)因子分解法、椭圆曲线因子分解法、数域筛(Number Field Sieve)因子分解法等。
3. ElGamal公钥密码
ElGamal公钥密码体制由T.ElGamal于1985年提出,该体制基于有限域上离散对数问题,既可用于加密,又可以用于数字签名。由于其较好的安全性,且同一明文在不同的时刻会生成不同的密文,在实际中得到了广泛的应用,尤其在数字签名方面的应用,著名的美国数字签名标准(DSS,Digital Signature Standard)其实就是ElGamal签名方案的一种变形。
(1)公私密钥对生成
随机选择一个大素数$p$,且要求$p-1$有大素数因子,$Z_p$是一个本原元($Z_p$ 是一个有$p$个元素的有限域,$Z_p^*$是$Z_p$中的非零元构成的乘法群)
选一个随机数$ x(1<x<p-1) $作为私钥,计算$y\equiv g^x $ $ mod $ $ p$, 公钥为 $ ( y, g, p)$
(2)加解密算法
- 公钥:($y,g,p)$
- 私钥:$x$
- 加密:$C=(c,c^{\prime})$,其中$c\equiv g^r $ $mod$ $ p $, $c^{^{\prime}}\equiv my^r $ $mod$ $ p$
- 解密:$m\equiv( \frac{c^{\prime}}{c^{x}} ) mod p$
ElGamal公钥密钥体制每次加密运算需要选择一个随机数,密文既依赖于明文,又依赖于选择的随机数,因此对于同一个明文,不同的时刻生成的密文不同。
此外,ElGamal加密使得消息扩展了两倍,即密文的长度是对应明文长度的两倍。